Understanding calorimetry is fundamental to mastering thermodynamics, a cornerstone of physical chemistry. Central to this understanding is the ability to calculate the calorimeter constant, a crucial value that quantifies the heat capacity of the calorimeter itself. Bomb calorimeters, specialized devices used to measure the heat of combustion, require a precisely determined calorimeter constant for accurate results. Scientists at reputable institutions like NIST use precise methodology to calculate the calorimeter constant for their instruments and in their advanced material testing. Accurate measurements within the calorimeter are vital for research, so correctly applying the specific heat capacity of the solution is key to calculate the calorimeter constant.
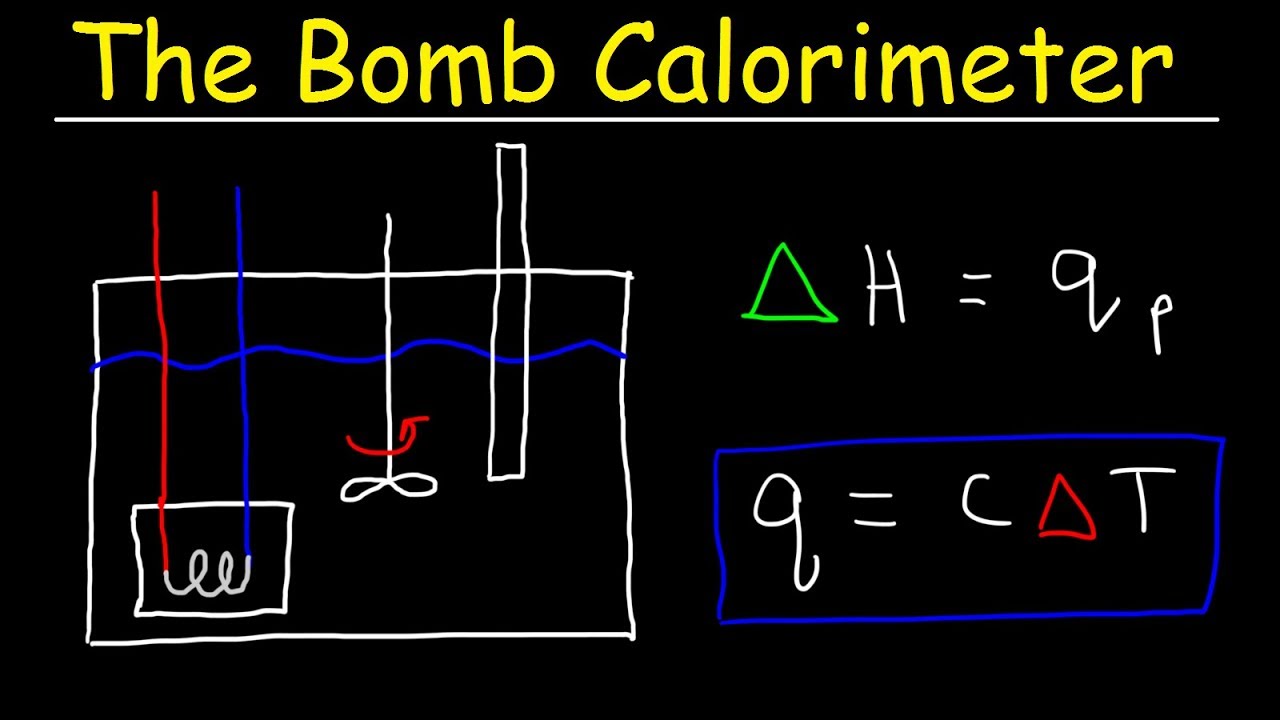
Image taken from the YouTube channel The Organic Chemistry Tutor , from the video titled Bomb Calorimeter vs Coffee Cup Calorimeter Problem – Constant Pressure vs Constant Volume Calorimet .
Mastering Calorimetry: Calculating the Calorimeter Constant Like a Pro!
Calorimetry is the science of measuring the heat of chemical reactions or physical changes. At the heart of many calorimetry experiments lies a crucial value: the calorimeter constant. This constant accounts for the heat absorbed by the calorimeter itself (the container and its components) during a reaction. Knowing how to calculate the calorimeter constant accurately is essential for obtaining reliable results. This guide will walk you through the process step-by-step.
Why is the Calorimeter Constant Important?
A calorimeter isn’t perfectly insulated. It absorbs some heat from the reaction or process being studied. This absorbed heat doesn’t contribute to the temperature change of the solution within the calorimeter, but it does affect the overall energy balance. The calorimeter constant (often denoted as ‘C’) quantifies how much heat is required to change the calorimeter’s temperature by one degree Celsius (or Kelvin). Ignoring this constant will lead to inaccurate calculations of the heat evolved or absorbed by the reaction.
Understanding the Formula and Key Variables
The fundamental concept for calculating ‘C’ involves introducing a known amount of heat into the calorimeter and measuring the resulting temperature change. We can then use the following equation:
Q = C * ΔT
Where:
- Q represents the heat added to the calorimeter (in Joules, J, or calories, cal).
- C is the calorimeter constant (in J/°C or cal/°C).
- ΔT is the change in temperature (in °C).
To calculate the calorimeter constant, we rearrange the formula:
C = Q / ΔT
Methods to Determine the Calorimeter Constant
Several methods can be used to determine the calorimeter constant. The most common involves the addition of a known amount of heat, typically through the mixing of warm and cold water. Another method involves electrical heating. Let’s explore these:
Method 1: Mixing Warm and Cold Water
This is a straightforward and commonly used technique. It relies on the principle of heat transfer between two water samples at different temperatures.
-
Prepare the Calorimeter: Start by adding a known mass of cold water (mcold) to the calorimeter. Record its initial temperature (Tcold). Ensure thorough mixing to get an accurate reading.
-
Heat the Warm Water: Heat a known mass of warm water (mwarm) and carefully record its initial temperature (Twarm).
-
Mix and Monitor: Quickly transfer the warm water into the calorimeter containing the cold water. Gently stir the mixture to ensure uniform temperature distribution.
-
Record Final Temperature: Carefully monitor the temperature of the mixture until it stabilizes. Record this final temperature (Tfinal). This is the equilibrium temperature reached after the heat exchange.
-
Calculate the Heat Transfer (Q): We assume that the heat lost by the warm water is equal to the heat gained by the cold water plus the heat gained by the calorimeter. This is the core principle:
- Heat lost by warm water: Qwarm = mwarm c (Twarm – Tfinal)
- Heat gained by cold water: Qcold = mcold c (Tfinal – Tcold)
- Where ‘c’ is the specific heat capacity of water (approximately 4.186 J/g°C or 1 cal/g°C).
Since Heat lost = Heat Gained:
Qwarm = Qcold + Qcalorimeter
Qcalorimeter = Qwarm – Qcold -
ÔªøCalculate the Calorimeter Constant (C):
C = Qcalorimeter / ΔT
Where ΔT = Tfinal – Tcold
Example Calculation:
Let’s say:
- mcold = 100 g
- Tcold = 20 °C
- mwarm = 100 g
- Twarm = 50 °C
- Tfinal = 34 °C
- c = 4.186 J/g°C
Then:
- Qwarm = 100 g 4.186 J/g°C (50 °C – 34 °C) = 6697.6 J
- Qcold = 100 g 4.186 J/g°C (34 °C – 20 °C) = 5860.4 J
- Qcalorimeter = 6697.6 J – 5860.4 J = 837.2 J
- ΔT = 34 °C – 20 °C = 14 °C
- C = 837.2 J / 14 °C = 59.8 J/°C (approximately)
Method 2: Electrical Heating
This method uses a calibrated electrical heater immersed in the calorimeter to deliver a known amount of heat.
-
Set Up: Place a known mass of water in the calorimeter. Ensure the electrical heater is fully submerged. Record the initial temperature of the water (Tinitial).
-
Apply Heat: Turn on the heater and record the voltage (V) and current (I) flowing through it. Note the time (t) in seconds for which the heater is on.
-
Monitor Temperature: Continuously monitor the temperature of the water in the calorimeter until it reaches a stable, final temperature (Tfinal).
-
Calculate the Heat (Q): The heat added electrically is calculated using the following formula:
Q = V I t
Where:
- V is the voltage (in Volts)
- I is the current (in Amperes)
- t is the time (in seconds)
-
ÔªøCalculate the Calorimeter Constant (C):
C = (Q – m c ΔT) / ΔTWhere:
- m is the mass of water
- c is the specific heat capacity of water
- ΔT = Tfinal – Tinitial
Important Considerations for Both Methods:
- Stirring: Consistent stirring is crucial for uniform temperature distribution.
- Insulation: Minimize heat loss to the surroundings by ensuring the calorimeter is well-insulated.
- Temperature Accuracy: Use a high-precision thermometer to measure temperatures accurately.
- Water Purity: Use distilled or deionized water to avoid impurities affecting the results.
- Repeat Measurements: Perform multiple trials and average the results to improve accuracy and reduce random errors.
Factors Affecting Accuracy
Several factors can influence the accuracy of your calorimeter constant determination. Here’s a quick breakdown:
| Factor | Impact | Mitigation Strategy |
|---|---|---|
| Heat Loss/Gain to Surroundings | Inaccurate heat measurements; leads to an over/underestimated constant. | Use a well-insulated calorimeter; minimize the duration of the experiment. |
| Inaccurate Temperature Readings | Errors in ΔT lead to errors in ‘C’. | Use a calibrated, high-precision thermometer; ensure thorough mixing before taking readings. |
| Impure Water | Changes in specific heat capacity can affect calculations. | Use distilled or deionized water. |
| Incomplete Mixing | Non-uniform temperature distribution; leads to inaccurate readings. | Ensure thorough and consistent stirring. |
By understanding these factors and taking appropriate precautions, you can significantly improve the accuracy of your calorimeter constant calculation. This will lead to more reliable results in all your calorimetry experiments.
Mastering Calorimetry: FAQs
What exactly is the calorimeter constant, and why is it important?
The calorimeter constant (often represented as C) represents the heat capacity of the calorimeter itself. It’s the amount of heat required to raise the calorimeter’s temperature by 1 degree Celsius (or Kelvin). Knowing it allows you to Ôªøcalculate the calorimeter constantÔªø and account for heat absorbed or released by the calorimeter during a reaction. This ensures accurate measurements of the heat involved in the reaction itself.
How does the calorimeter constant affect my calculations?
If you ignore the calorimeter constant, you’re assuming all the heat released or absorbed by the reaction is going directly into the solution inside the calorimeter. In reality, some heat is used to change the temperature of the calorimeter. When you accurately Ôªøcalculate the calorimeter constantÔªø, you’re acknowledging that you need to account for the heat it absorbs to be precise.
What are some common methods to determine the calorimeter constant?
One common method involves adding a known amount of heat to the calorimeter (e.g., adding a hot metal of known mass and specific heat). Then, you carefully measure the temperature change. By relating the heat added to the temperature change, you can Ôªøcalculate the calorimeter constantÔªø using the formula: C = Q / ΔT, where Q is the heat added and ΔT is the change in temperature.
Is the calorimeter constant the same for all calorimeters?
No, the calorimeter constant is specific to each individual calorimeter. Factors like the calorimeter’s material, construction, and insulation affect its heat capacity. That is why it is crucial to experimentally determine the calorimeter constant for each calorimeter you use. To get accurate data, you must Ôªøcalculate the calorimeter constantÔªø with care for each unique set-up.
Alright, you’ve got a solid grasp on how to calculate the calorimeter constant! Now go put that knowledge to use and remember, practice makes perfect. Happy experimenting!