Understanding the fcc number of atoms requires a grasp of its underlying crystal structure. This arrangement significantly impacts a material’s properties, making it a crucial concept in materials science. X-ray diffraction, a powerful analytical technique, allows scientists to experimentally determine this structure. The face-centered cubic (FCC) lattice, a common arrangement found in elements such as aluminum and copper, has a specific fcc number of atoms that defines its density and reactivity.
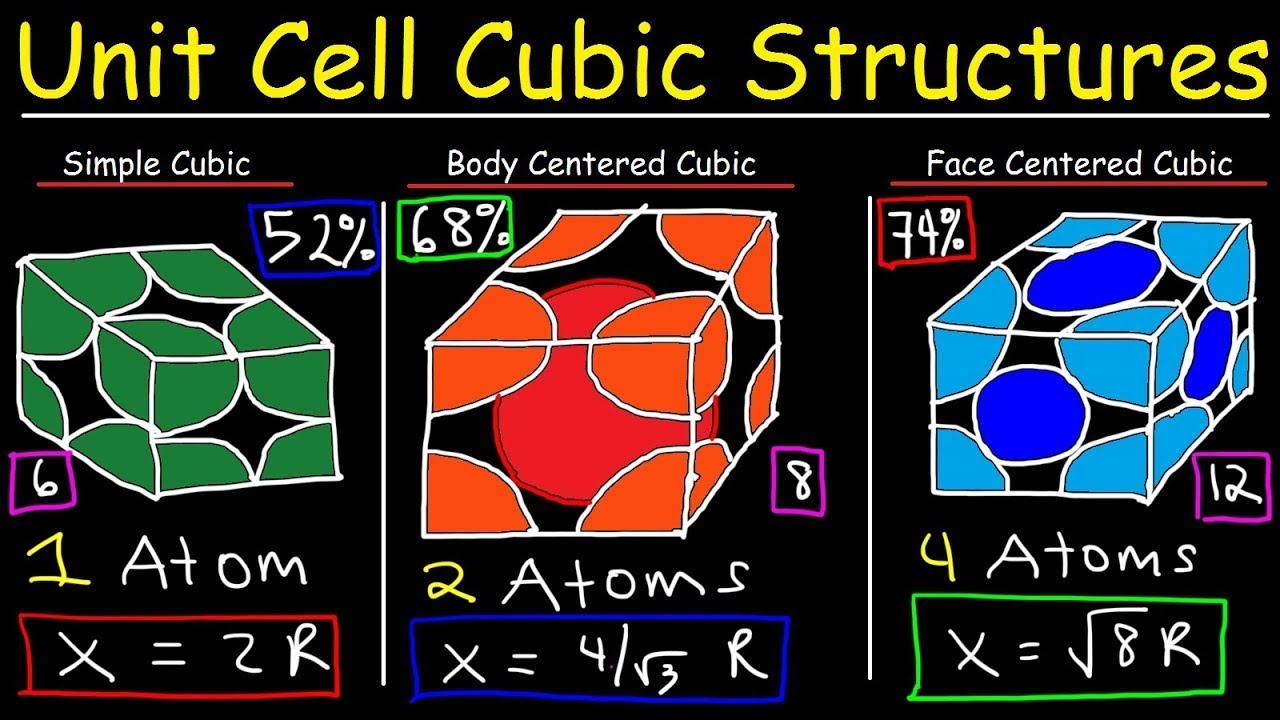
Image taken from the YouTube channel The Organic Chemistry Tutor , from the video titled Unit Cell Chemistry Simple Cubic, Body Centered Cubic, Face Centered Cubic Crystal Lattice Structu .
Understanding the FCC Number of Atoms: A Deep Dive
The face-centered cubic (FCC) crystal structure is a common arrangement of atoms in many metals and other materials. Determining the "fcc number of atoms" within a unit cell is fundamental to understanding its properties. This article breaks down the concept step-by-step, providing clarity on how this number is calculated.
What is the FCC Crystal Structure?
Before delving into calculating the number of atoms, it’s important to establish what defines an FCC structure.
Key Characteristics of FCC
- Cubic Unit Cell: The basic repeating unit is a cube.
- Atoms at Corners: An atom sits at each of the eight corners of the cube.
- Atoms on Faces: An atom is located at the center of each of the six faces of the cube.
Visualizing the Structure
Imagine a cube. Now, picture an atom placed at each of its corners. Finally, visualize another atom sitting right in the middle of each of the six faces of that cube. That’s an FCC unit cell.
Calculating the FCC Number of Atoms
The key to calculating the "fcc number of atoms" lies in understanding how atoms are shared between unit cells.
Corner Atoms Contribution
Each corner atom is shared by eight adjacent unit cells. Therefore, only 1/8th of each corner atom actually belongs to a particular unit cell.
- Number of corner atoms: 8
- Contribution per corner atom: 1/8
- Total contribution from corner atoms: 8 * (1/8) = 1 atom
Face-Centered Atoms Contribution
Each face-centered atom is shared by two adjacent unit cells. This means only 1/2 of each face-centered atom belongs to a particular unit cell.
- Number of face-centered atoms: 6
- Contribution per face-centered atom: 1/2
- Total contribution from face-centered atoms: 6 * (1/2) = 3 atoms
The Total Number of Atoms
To determine the "fcc number of atoms", we simply add the contributions from the corner atoms and the face-centered atoms.
- Total number of atoms in an FCC unit cell: 1 (from corners) + 3 (from faces) = 4 atoms
In summary, an FCC unit cell contains effectively four atoms.
Why is the FCC Number of Atoms Important?
Knowing the "fcc number of atoms" allows us to calculate various important properties of materials with an FCC structure.
Density Calculations
The density of a material depends on the number of atoms packed into a given volume. Knowing the number of atoms in the unit cell, its volume, and the atomic mass of the element allows for accurate density calculations.
Understanding Material Properties
The arrangement of atoms in an FCC structure, and thus the "fcc number of atoms", significantly influences a material’s mechanical, electrical, and thermal properties. For example, FCC metals tend to be ductile and malleable due to the ease with which atoms can slip past each other in this structure.
Examples of FCC Structures
Many common metals adopt the FCC crystal structure. Here’s a small selection:
| Metal | Notes |
|---|---|
| Aluminum | Widely used in aerospace and packaging |
| Copper | Excellent electrical conductivity |
| Gold | Highly resistant to corrosion |
| Silver | Good electrical and thermal conductor |
| Nickel | Used in many alloys for strength |
FAQs: Understanding the FCC Number of Atoms
This FAQ section addresses common questions about the Face-Centered Cubic (FCC) crystal structure and calculating its number of atoms. We hope this provides further clarity on this important concept in materials science.
How many atoms are contained within a single FCC unit cell?
The fcc number of atoms in a unit cell is four. This arises from each corner atom contributing 1/8 and each face-centered atom contributing 1/2 to the unit cell count. Eight corners 1/8 + six faces 1/2 = 4 atoms.
Why do corner atoms only contribute 1/8 to the FCC unit cell?
Corner atoms are shared by eight adjacent unit cells in the crystal lattice. Therefore, only one-eighth of each corner atom resides within a given unit cell. This is essential for accurately determining the fcc number of atoms.
What is the significance of knowing the FCC number of atoms?
Knowing the fcc number of atoms is crucial for calculating various material properties. These include density, atomic packing factor, and understanding the material’s behavior under different conditions. It directly impacts materials design and engineering applications.
How does the FCC structure differ from other crystal structures like BCC and HCP in terms of atom count?
The FCC structure contains 4 atoms per unit cell. In contrast, BCC (Body-Centered Cubic) contains 2 atoms, and HCP (Hexagonal Close-Packed) contains 6 atoms per unit cell. This difference in atom count affects the fcc number of atoms and consequently the density and other properties.
So, hopefully, that cleared up the mystery around the fcc number of atoms! Now you have a better understanding of how those atoms are arranged and why it matters. Keep exploring those cool materials!