The quadratic equation, a fundamental concept in algebra, often presents a challenge. This guide will clarify how to calculate quadratic equation effectively, even if you’re unfamiliar with Desmos, a helpful graphing calculator. The method of factoring, a common problem-solving technique, is fully explain. The Pythagorean theorem is an easy example of how quadratic equations are useful.
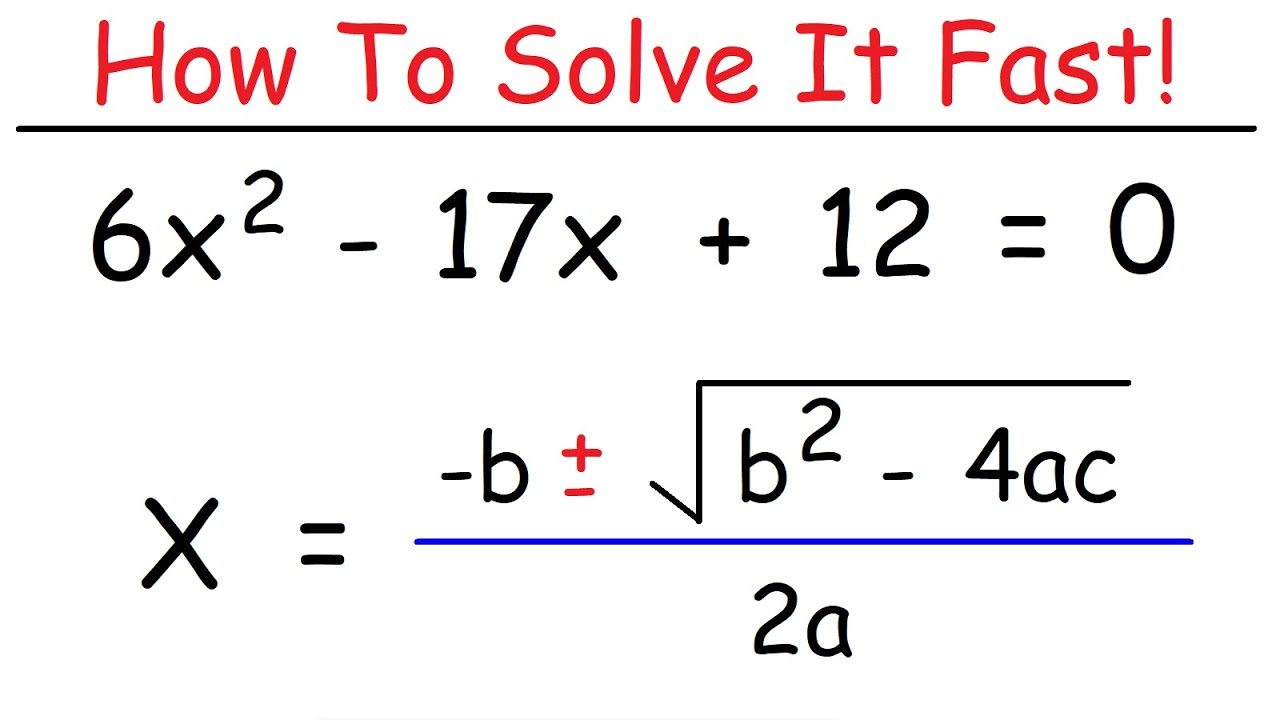
Image taken from the YouTube channel The Organic Chemistry Tutor , from the video titled How To Solve Quadratic Equations Using The Quadratic Formula .
Decoding the Quadratic Equation: Your Simple Calculation Guide
This guide breaks down how to calculate quadratic equations, making them understandable and manageable. We’ll cover the basics, explore the different methods, and provide examples to help you master this essential mathematical tool.
Understanding the Basics of Quadratic Equations
What is a Quadratic Equation?
A quadratic equation is a polynomial equation of the second degree. This simply means the highest power of the unknown variable (usually ‘x’) is 2. The standard form is:
ax² + bx + c = 0
Where:
- ‘a’, ‘b’, and ‘c’ are constants (numbers), and
- ‘x’ is the variable.
- ‘a’ cannot be zero, otherwise it becomes a linear equation.
Identifying ‘a’, ‘b’, and ‘c’
Being able to correctly identify ‘a’, ‘b’, and ‘c’ is the first crucial step. Let’s look at some examples:
- Example 1: 3x² + 5x – 2 = 0. Here, a = 3, b = 5, and c = -2.
- Example 2: x² – 4x = 0. Here, a = 1, b = -4, and c = 0. (Remember that if a term isn’t explicitly written, its coefficient is 1 or 0).
- Example 3: 2x² + 7 = 0. Here, a = 2, b = 0, and c = 7.
Methods to Calculate Quadratic Equation Solutions
There are three primary methods for solving quadratic equations:
- Factoring
- Completing the Square
- Using the Quadratic Formula
Method 1: Factoring
Factoring involves expressing the quadratic equation as a product of two binomials. This method is only suitable for certain types of quadratic equations that can be easily factored.
How to Factor
- Rewrite the equation in standard form: ax² + bx + c = 0.
- Find two numbers: that multiply to ‘ac’ and add up to ‘b’.
- Rewrite the middle term (‘bx’): using the two numbers you found.
- Factor by grouping: Group the terms and factor out the greatest common factor from each group.
- Set each factor to zero: and solve for ‘x’.
Factoring Example
Let’s solve x² + 5x + 6 = 0 by factoring.
- ‘ac’ is 1 * 6 = 6. ‘b’ is 5.
- We need two numbers that multiply to 6 and add to 5. These numbers are 2 and 3.
- Rewrite the equation: x² + 2x + 3x + 6 = 0.
- Factor by grouping:
- x(x + 2) + 3(x + 2) = 0
- (x + 2)(x + 3) = 0
- Set each factor to zero:
- x + 2 = 0 => x = -2
- x + 3 = 0 => x = -3
Therefore, the solutions are x = -2 and x = -3.
Method 2: Completing the Square
Completing the square is a more general method that can be used to solve any quadratic equation, even those that are difficult to factor.
How to Complete the Square
- Rewrite the equation: ax² + bx = -c
- Divide by ‘a’ (if a ≠ 1): x² + (b/a)x = -c/a
- Calculate (b/2a)²: This is the value that needs to be added to both sides.
- Add (b/2a)² to both sides: x² + (b/a)x + (b/2a)² = -c/a + (b/2a)²
- Rewrite the left side as a perfect square: (x + b/2a)² = -c/a + (b/2a)²
- Take the square root of both sides: x + b/2a = ±√(-c/a + (b/2a)²)
- Solve for ‘x’: x = -b/2a ± √(-c/a + (b/2a)²)
Completing the Square Example
Let’s solve x² + 6x + 5 = 0 by completing the square.
- x² + 6x = -5
- ‘a’ is already 1.
- (b/2a)² = (6/2)² = 3² = 9
- x² + 6x + 9 = -5 + 9
- (x + 3)² = 4
- x + 3 = ±√4 => x + 3 = ±2
- x = -3 ± 2
Therefore, the solutions are x = -3 + 2 = -1 and x = -3 – 2 = -5.
Method 3: Using the Quadratic Formula
The quadratic formula is a direct formula to find the solutions to any quadratic equation. It is derived from the completing the square method.
The Quadratic Formula
Given ax² + bx + c = 0, the solutions for ‘x’ are given by:
x = [-b ± √(b² – 4ac)] / 2a
Understanding the Discriminant
The term inside the square root, b² – 4ac, is called the discriminant. It tells us about the nature of the solutions:
| Discriminant (b² – 4ac) | Nature of Solutions |
|---|---|
| Positive (b² – 4ac > 0) | Two distinct real solutions |
| Zero (b² – 4ac = 0) | One real solution (repeated root) |
| Negative (b² – 4ac < 0) | Two complex (non-real) solutions |
Quadratic Formula Example
Let’s solve 2x² – 5x + 3 = 0 using the quadratic formula.
- Identify a = 2, b = -5, and c = 3.
- Plug the values into the formula:
x = [-(-5) ± √((-5)² – 4 2 3)] / (2 * 2)
x = [5 ± √(25 – 24)] / 4
x = [5 ± √1] / 4
x = [5 ± 1] / 4
- Calculate the two possible values for x:
x₁ = (5 + 1) / 4 = 6 / 4 = 3/2
x₂ = (5 – 1) / 4 = 4 / 4 = 1
Therefore, the solutions are x = 3/2 and x = 1.
Choosing the Right Method
| Method | Advantages | Disadvantages | When to Use |
|---|---|---|---|
| Factoring | Simple and quick when the equation is easily factorable. | Not all quadratic equations can be easily factored. | When the equation can be easily factored. |
| Completing the Square | Can be used for any quadratic equation. Useful for deriving formulas. | Can be more complex and time-consuming than other methods. | When the equation is not easily factored or when asked to solve using this method. |
| Quadratic Formula | Works for all quadratic equations. Straightforward application. | Can be prone to errors if signs or values are substituted incorrectly. | When factoring is difficult or impossible, or for a quick, guaranteed solution. |
FAQs: Understanding the Quadratic Equation
Here are some common questions about quadratic equations and how to solve them using the quadratic formula.
What exactly is a quadratic equation?
A quadratic equation is a polynomial equation of the second degree. It generally takes the form ax² + bx + c = 0, where a, b, and c are constants, and ‘a’ is not equal to zero.
Why is it important to know how to calculate quadratic equations?
Quadratic equations appear in many areas of math, physics, engineering, and other fields. Knowing how to solve them is essential for solving a variety of real-world problems. Plus, it builds a foundation for understanding more complex equations.
What is the most reliable way to solve a quadratic equation?
The quadratic formula is the most reliable method. This formula, x = [-b ± √(b² – 4ac)] / 2a, always provides the correct solutions, even when factoring is difficult or impossible. Using the quadratic formula is often the fastest way to calculate quadratic equation roots.
What does the discriminant (b² – 4ac) tell me about the solutions?
The discriminant reveals the nature of the roots. If b² – 4ac > 0, there are two distinct real roots. If b² – 4ac = 0, there is exactly one real root (a repeated root). And if b² – 4ac < 0, there are two complex roots. Knowing this beforehand can help when you calculate quadratic equation outcomes.
Alright, that’s a wrap on unlocking the secrets of how to calculate quadratic equation! Go forth and conquer those problems – you’ve got this!